Pośrednie dowody na istnienie nieznanej planety w Układzie Słonecznym
Profesorowie Konstantin Batygin i Mike Brown z Caltechu (California Institute of Technology) twierdzą, że w Układzie Słonecznym istnieje dziewiąta, nieznana jeszcze, planeta. Jej masa ma być 10-krotnie większa od masy Ziemi, a planeta ma znajdować się średnio w odległości 20-krotnie większej od Słońca niż Neptun. Jej obieg wokół naszej gwiazdy ma trwać 10-20 tysięcy lat. Problem jednak w tym, że Batygin i Brown nie zaobserwowali opisywanej przez siebie planety.
Obaj uczeni wykorzystali modelowanie matematyczne i symulacje komputerowe. To na ich podstawie mówią o obecności nieznanej planety. Od czasów starożytnych odkryto jedynie dwie planety. Ta byłaby trzecia. To znaczący fragment Układu Słonecznego, który czeka na odkrycie - mówi profesor Brown.
Naukowiec podkreśla, że obiekt, o którym mowa, z pewnością zostałby zaliczony do planet. Jest bowiem 5000 razy bardziej masywny od Plutona, który niedawno stracił miano planety. Dziewiąta planeta dominuje grawitacyjnie nad swoim otoczeniem, a biorąc pod uwagę wielkość jej orbity, trzeba stwierdzić, że dominuje ona nad większym obszarem niż jakakolwiek inna planeta Układu Słonecznego.
Batygin i Brown opisali swoje obliczenia na łamach Astronomical Journal. Zauważają oni, że obecność dziewiątej planety wyjaśnia wiele tajemnic Pasa Kuipera. Początkowo sceptycznie podchodziliśmy do pomysłu istnienia tej planety, jednak w miarę badania jej orbity oraz wpływu na zewnętrzne regiony Układu Słonecznego byliśmy coraz bardziej przekonani, że ona istnieje. Po raz pierwszy od 150 lat pojawił się solidny dowód na to, że spis planet Układu Słonecznego jest niepełny - mówi profesor Batygin.
Badania Browna i Batygina zostały zainspirowane pracą byłego doktoranta profesora Browna. Chad Trujillo i jego kolega, Scott Sheppard, opublikowali pracę, w której stwierdzili, że orbity 13 z najbardziej odległych obiektów Pasa Kuipera mają podobne cechy, a podobieństwa te może wyjaśnić obecność niewielkiej planety. Profesor Brown uznał, że to mało prawdopodobne, ale nawiązał współpracę z profesorem Batyginem i przez 1,5 roku badali wspomniane obiekty z Pasa Kuipera. Brown, który bardziej polega na obserwacjach, próbował ułożyć wszystko w kontekście tego, co obserwowalne, z kolei teoretyk Batygin większy nacisk kładł na kontekst fizyczny i dynamikę badanych układów. Dzięki tej różnicy podejść mogli nawzajem weryfikować swoje spostrzeżenia. Ja mówiłem o tym, co zaobserwowałem, on używał argumentów teoretycznych i w ten sposób się spieraliśmy. Nie sądzą, byśmy mogli cokolwiek osiągnąć bez takiego wzajemnego spierania się - mówi Brown.
Uczeni dość szybko zdali sobie sprawę z faktu, że sześć z trzynastu obiektów wspomnianych przez Trujillo i Shepparda ma eliptyczne orbity zwrócone w tym samym kierunku przestrzeni. To tak, jakbyśmy mieli sześć wskazówek zegarka, z których każda porusza się z różną prędkością, ale gdy na nie spojrzymy, to akurat wszystkie są w tym samym miejscu, mówi Brown, podkreślając, że prawdopodobieństwo takiego wydarzenia wynosi 1:100. Jednak to nie wszystko. Orbity wszystkich tych obiektów są identycznie nachylone pod kątem 30 stopni w dół w stosunku do płaszczyzny ekliptyki. Prawdopodobieństwo, że taki ułożenie jest przypadkowe, wynosi 0,007%. To nie powinno się wydarzyć. Pomyśleliśmy, że coś nadało kształt ich orbitom, stwierdził Brown.
Początkowo naukowcy sądzili, że tym czymś są jakieś nieodkryte jeszcze obiekty z Pasa Kuipera. Szybko jednak odrzucili tę możliwość, gdy Pas musiałby mieć masę 100-krotnie większą niż obecnie. Uczeni postanowili więc symulować obecność planety. Obliczenia wykazały, że wpłynęłaby ona na wspomniane obiekty, jednak nie do końca tak, jak się one zachowywały.
Później, przez przypadek, Batygin i Brown zdali sobie sprawę, że gdyby symulowana przez nich planeta miała zupełnie inną orbitę, taką, której peryhelium jest nachylone pod kątem 180 stopni do peryhelium wszystkich innych obiektów Układu Słonecznego, to wywarłaby taki wpływ na wspomnianych sześć obiektów, jaki obserwujemy. Na pierwszy rzut oka taki układ nie może być stabilny w dłuższym czasie, ponadto doprowadziłby do kolizji pomiędzy hipotetyczną planetą, a obiektami. Jednak jeśli weźmiemy pod uwagę fakt, że w czasie gdy dziewiąta planeta obiegnie Słońce czterokrotnie, odległe obiekty z Pasa Kuipera zakończą 9 orbit, to do kolizji nigdy nie dojdzie. Planeta będzie jedynie wpływała na obiekty tak, że ich konfiguracja w stosunku do niej zostanie zachowana.
Dalsze symulacje i coraz bardziej szczegółowe obliczenia wykazały, że obecność dziewiątej planety wyjaśniałaby również niezwykłą orbitę Sedny, która - w przeciwieństwie do innych obiektów z Pasa, nigdy nie zbliża się do Neptuna. Podobnie zachowuje się obiekt 2012 VP113. Z wyliczeń wynika, że Sedna, 2012 VP113 i - potencjalnie - inne obiekty z Pasa Kuipera mogą pod wpływem dziewiątej planety zmieniać swoje orbity na mniej związane z Neptunem.
Jednak tym, co ostatecznie przekonało Batygina i Browna było wyliczenie, że w Pasie Kuipera powinny znajdować się obiekty nachylone prostopadle do płaszczyzny planet. W ciągu ostatnich trzech lat znaleziono cztery takie obiekty.
Skąd wzięła się dziewiąta planeta? Obecnie dominuje teoria, że historia Układu Słonecznego rozpoczęła się od czterech planetarnych rdzeni, wokół których z czasem powstały Jowisz, Saturn, Uran i Neptun. Z czasem wskutek wzajemnych oddziaływań i kolizji znalazły się one na obecnych orbitach, powstały też pozostałe planety. Nie ma jednak żadnego powodu, dla którego nie miałoby istnieć pięć takich rdzeni planetarnych. Dziewiąta planeta może być właśnie piątą z oryginalnych planet Układu Słonecznego. Jeśli znalazła się w pewnym momencie zbyt blisko Jowisza lub Saturna mogła zostać wyrzucona na odległą ekscentryczną orbitę.
Astronomowie już przystąpili do poszukiwania dziewiątej. Jeśli obecnie znajduje się ona w dużej odległości od Słońca, zaobserwować ją będzie można jedynie za pomocą teleskopów Kecka czy Subaru. Jeśli jest bliżej, powinno ją zobaczyć wiele teleskopów.


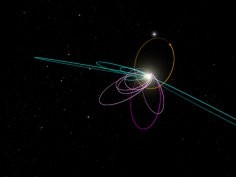
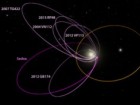


Komentarze (36)
wilk, 21 stycznia 2016, 16:03
Trochę duża jak na taki dystans...
Jajcenty, 21 stycznia 2016, 16:22
No. Aż sprawdzałem na wiki bo 600 ja to nie w kij dmuchał.
Gość Astro, 21 stycznia 2016, 16:41
Praca śliczniutka i ciekawa (oryginalny oryginał: http://iopscience.iop.org/article/10.3847/0004-6256/151/2/22/pdf), polecam jednak rozwadze drugi rysuneczek na Kopalni. Wielkie półosie 6 (z 13) rozpatrywanych KBO ograniczone są (tak na oko) przez kąt prosty. Jakiś ignorant (jak ja) może głupio zapytać, jakie jest prawdopodobieństwo (losowy rzut 13 kamyczków) trafienia 6 kamyczków w jedną ćwiartkę 2D Kartezjusza ( )?
)?
Jako abisalnie nieogarnięty ekscentryk (ludź może być ekscentryczny, orbita NIE ) muszę nadmienić, że orbity są mniej ± bardziej kołowe/ eliptyczne. Eccentricity vs mimośród. Niezły łamaniec językowy.
) muszę nadmienić, że orbity są mniej ± bardziej kołowe/ eliptyczne. Eccentricity vs mimośród. Niezły łamaniec językowy. 
Jajcenty, 21 stycznia 2016, 17:18
w dokładnie jedną wybraną ćwiartkę:
(13 po 6) * (1/4)6 * (3/4)7
czyli coś koło: 0,0559 ale w dowolną już cztery razy większe: 0,2237
A jednak zjawisk grawitacyjnych nie rozważałbym w kategoriach prawdopodobieństwa.
Gość Astro, 21 stycznia 2016, 17:38
Brawo Jajcenty (nie sprawdzam rachunków, bo komu, jak komu ale Tobie nie można nie ufać). Mamy zatem inne ciekawe zadanie: czy wszyscy zgadzają się, nie z rachunkami, ale założeniami Jajcentego?
Spróbuję delikatnie: a jednak!
Jajcenty, 21 stycznia 2016, 17:44
No tak, w takim US wszystko w jednej płaszczyźnie, wiruje w jednym kierunku, dorobiło się Keplera i w ogóle oszalały determinizm po całości.
Na moje wyczucie to jak rzucić garścią kółek zębatych o ścianę i dostać Omegę.
Gość Astro, 21 stycznia 2016, 17:52
Nie sądzę.
Niekoniecznie.
No tak mają pewni wyznawcy.

ex nihilo, 21 stycznia 2016, 18:22
Na zmarznięty łeb (po cholerę te zwierzaki mają mordy, flaki i dupska???) wychodzi mi 0,00003258(9) dla dokładnie 6 i 0,00024414(1) dla ≥ 6. Byndzie?
W przypadku wybranej jedno i drugie *0,25.
Gość Astro, 21 stycznia 2016, 19:08
Poczułem się nieswojo… Nihilo i Jajcenty: przyznam szczerze, że jeszcze nie chciało mi się za to wziąć…
Wygląda zwyczajnie na ciekawe zadanie z prawdopodobieństwa, choć mam swoje (być może "pseudo") typowanie.
Jeśli któremuś z Was wydaje się, że macie Pewność, to warto (może krótko ) o dobrą iskierkę, czyli taką tam logiczną argumentację.
) o dobrą iskierkę, czyli taką tam logiczną argumentację. 
ex nihilo, 21 stycznia 2016, 19:30
Pewności nie mam (w chałupie też zimno jak cholera, dopiero w piecu rozpaliłem), to i argumentacji nie bedę dawał, bo mogłaby w krzaczory skierować Nie sprawdzałem też tego (inne przypadki, krzywa).
Nie sprawdzałem też tego (inne przypadki, krzywa).
Jajcenty, 21 stycznia 2016, 19:33
Ja użyłem rozkładu dwumianowego nie mając pewności co do natury (rozkładu) zjawiska. To mój dylemat od czasu matury: strzelec trafia z prawdopodobieństwem 0,9 oblicz ile razy musi strzelić by prawdopodobieństwo trafienia było nie mniejsze niż 0,99. Wszyscy używają Bernouliego, mimo że wszyscy wiedzą, że strzelanie podlega Gausowi.
Centralne pytanie czy wolno używać dwumianowego tylko dlatego, że odróżniamy sukces od porażki?
Nie. To drugie jest o rząd za duże. Intuicja brydżysty.
tempik, 21 stycznia 2016, 19:50
no niezła orbita.... pewne z powierzchni takiej planety bez wsparcia porządnej optyki nie da się stwierdzić która gwiazdka na niebie to gwiazda macierzysta
Ortolan, 21 stycznia 2016, 20:01
Każde badania, nie tylko astronomiczne, powinny być prowadzone w podobny sposób jak w tym przypadku. Gdzie nad danym zagadnieniem pracuje co najmniej dwóch ludzi o różnym podejściu czy poglądach i wzajemnie starają się wykluczać swoje teorie lub wprowadzać swoje pomysły. Konstruktywna krytyka i burza mózgów to najlepsze co może przytrafić się nauce.
Nie mam zbyt dużej wiedzy astronomicznej, ale trochę odnoszę wrażenie, że w tym przypadku zadziałała autosugestia: Chcieli znaleźć planetę to ją znaleźli, wszystko dopasowali do tego żeby ona tam była. Życzę jednak żeby faktycznie nowa planeta okazała się prawdą, to będzie sensacja:)
ex nihilo, 21 stycznia 2016, 20:54
Raczej za małe, bo chyba trzeba by dodać rozkłady dla 7→13, ale wszystko mi się już teraz dokładnie chrzani.
Zadroszczę, bo kart w łapach nie miałem już > 30 lat.
Wychodzą mi dwa strzały... To już raczej z doświadczenia, chociaż też dosyć dawnego
To już raczej z doświadczenia, chociaż też dosyć dawnego 
radar, 21 stycznia 2016, 20:57
Też odniosłem takie wrażenie o autosugestii chociaż również czekam z niecierpliwością na potwierdzenie
Co do planety: a śmieli się, że Nibiru leci
Gość Astro, 21 stycznia 2016, 21:07
Adin, dwa, tri.
Czy rzut 13. kamykami musi oznaczać niezależność losową? Niekoniecznie jest to tożsame z 13. losowymi rzutami kamykiem. Chyba.
pogo, 21 stycznia 2016, 21:29
Cóż... Tych obiektów może być 1000 zupełnie różnych, ale znamy tylko 13 o podobnych orbitach, bo akurat tam patrzyliśmy. Choć to raczej mało prawdopodobne, bo z tego co kojarzę, to są bardzo daleko od siebie.
Ciekawiej by było jakby wykluczyli więcej możliwości (nie czytałem oryginalnego oryginału). Moim głównym podejrzanym byłby przelatujący akurat w pobliżu brązowy karzeł, a nie obiekt uwiązany na grawitacyjnej smyczy do naszej gwiazdy.
Jajcenty, 21 stycznia 2016, 21:29
0,00003258(9) dla dokładnie 6 i
0,00024414(1) dla ≥ 6. Byndzie
Urosło Ci osiem razy!
Rzucamy 13 kamyków w Kartezjusza, średnio spodziewamy się 13/4 = 3 i 1/4 kamienia w ćwiartce. To jest maks. Każde inne prawdopodobieństwo jest mniejsze
0,00003258(9) dla dokładnie 6
0,00000258(9) dla dokładnie 7
00000001000 dla dokładnie 8
....
00000000001 dla dokładnie 13
widzisz? chodzi mi o to że p. szybko maleje.
dla rozkładu dwumianowego wygląda to tak:
ex nihilo, 21 stycznia 2016, 22:29
Jak robiłem:
1, nie bawiłem się w takie czy inne rozkłady, bo dawno nie miałem z tym w sposób ścisły do czynienia, poza "intuicją gaussowską" (też dla kombinacji kilku rozkładów), ale tylko jakościowo, bez ilościowych rachunków. Inne też tylko jakościowo.
2. dla =6 przyjąłem, że pierwsze 6 musi trafić do jednej ćwiartki, czyli 0,256, a następne 7 do tej ćwiartki trafić nie może (0,757), zusammen do kupki: 0,256 * 0,757 = 0,00003258(9)
3. dla ≥6, z 7 kamieni zrobiłem "gaz kamieniowy" i rozłożyłem równo po ćwiartkach, czyli istotne było tylko pierwsze 6, wynik: 0,256 = 0,00024414(1)
(3) musi być większe od (2), bo nie ma ograniczenia dla nasŧepnych kamieni ("następne 7 do tej ćwiartki trafić nie może"), które mogą wpadać do dowolnej ćwiartki, też tej, w której jest już pierwsze 6. Jest tylko ograniczenie "dolne" =6. Czyli (3) musiało urosnąć w stosunku do (2).
Być może w tej partyzantce zrobiłem błąd, i to może niejeden, ale akurat tego, że: p(≥6) > p(=6) jestem pewny. Intuicja brydżowa nie musi się tu sprawdzać (zakladając jej poprawność), bo w brydżu masz ograniczenie =13kart, w których muszą się zmieścić rozklady wszystkich kolorów. Tutaj takiego ograniczenia nie ma - w ćwiartce może być 0→13 kamieni.
Edycja:
Faktycznie osiem razy to chyba za dużo... teraz tego nie wyłapię, muszę do końca rozmarznąć. Zap. mnie dzisiaj maksymalnie, miałem dosyć dużo do zrobienia na zewnątrz. Piec + koc elektryczny pod tyłkiem + 500W IR prosto w gębę jeszcze nie rozmroziło Byle do wiosny!
Byle do wiosny! 
Jajcenty, 21 stycznia 2016, 22:54
oczywiście będzie większe bo (2) jest dla 6 podczas gdy (3) = (2) + te dla większe od 6.
Jednak nie 8 razy!. Mam
I słusznie. Jednak 6 znajduje się mocno na prawo od średniej i intuicja podpowiada p(=6) > p(>6) zwróć uwagę, że łatwiej mi na ostrych nierównościach.
Bardzo dobrze!. Tylko to jest prawdopodobieństwo zdarzenia: pierwsze 6 sukcesów i potem 7 porażek. Ignorujesz np. 3 sukcesy, 3 porażki, 3 sukcesy, 4 porażki. W szczególności ignorujesz układ 7 porażek 6 sukcesów
Trzeba to jeszcze przemnożyć przez wszystkie permutacje, a raczej wariacje bez powtórzeń (13 po 6).
Reasumując liczysz jak ja tylko nie lubisz dwumianu Newtona ;p
Zesztą:
poznajesz? prawdopodobieństwo k sukcesów = pk(1-p)n-k a sukces może się zrealizować na (n k) sposobów.
ex nihilo, 21 stycznia 2016, 23:37
Wygląda na to, że masz rację, chciałem to za bardzo uprościć, no i w poślizg na zakręcie wpadłem :D
:D
Kurcze, ile to lat przerwy było... i co zabawne - czasem mniej problemów mam z bardziej skomplikowanymi zależnościami, niż z tymi prostymi, no i ta niechęć do kartki i ołówka
Edycja:
ale... czy tutaj kolejność (np. 3s,3p,3s,4p) i ilość kombinacji ma znaczenie? Zgodzimy się chyba, że p(13) = 0,2513, i że 1s ma p(1s) = 0,25, odpowiednio dla 1p: p(1p) = 0,75, czyli p(0) = 0,7513. Może mi się chrzani, ale w tym przypadku chyba nie ma znaczenia ani kolejność s i p, ani ilość możliwych kombinacji. Sam już nie wiem Muszę chyba kartkę wziąć, ale to już nie teraz
Muszę chyba kartkę wziąć, ale to już nie teraz 
pogo, 22 stycznia 2016, 01:25
Skup się na tych, które trafią do właściwej ćwiartki spośród tych 13. Prawdopodobieństwo, że dokładnie pozostałe nie trafią musi być identyczna, więc nie wolno mnożyć ani dodawać tych wartości. Można ich tylko użyć do weryfikacji obliczeń.
I to mniej więcej wszystko co pamiętam z liceum na temat prawdopodobieństwa... pomijając, fakt że przyda się tu dwumian Newtona. Z samej jego konstrukcji wynika symetria takich rozważań... wszak (6 nad 13) == (7 nad 13)
ex nihilo, 22 stycznia 2016, 11:42
Fujjj... znowu muszę wyjść na ten syf na zewnątrz... -3,5... kiedy wreszcie będzie +35?????????
Jajcenty, 22 stycznia 2016, 12:32
A bodaj by Cię... Mam nadzieję, że nigdy. Jak jest -35 to mogę założyć podkoszulek i zamknąć okno w łazience. Jak jest +35 to ze skóry już nie wyleze, pozostaje tylko stać pod prysznicem.