Padł rekord kwantowego rozkładu liczb

Chińscy fizycy pracujący pod kierunkiem Nanyanga Xu z Uniwersytetu Nauki i Technologii w Hefei pobili światowy rekord kwantowej faktoryzacji liczby.

Faktoryzacja, czyli rozkład liczby na czynniki pierwsze, których iloczyn daje tę liczbę, to podstawa łamania systemów kryptograficznych. Kryptografia korzysta z faktu, że przeprowadzenie faktoryzacji jest zajęciem niezwykle czasochłonnym. A z im większą liczbą mamy do czynienia, tym więcej czasu potrzeba na przeprowadzenie jej faktoryzacji. Stąd też wiemy, że im dane hasło jest dłuższe, tym jest trudniejsze do złamania. Dlatego też np. 128-bitowy szyfr będzie trudniejszy do złamania niż szyfr 64-bitowy.

Obecne techniki obliczeniowe nie pozwalają na złamanie bardzo długich szyfrów. Zajęłoby to bowiem zbyt dużo czasu.

Z zupełnie inną sytuacją mamy do czynienia w przypadku obliczeń kwantowych. One pozwoliłyby błyskawicznie dokonać wszelkich potrzebnych obliczeń i natychmiast złamać nawet najdłuższy tradycyjny szyfr.

Na razie jednak nie potrafimy kontrolować dużej liczby kubitów (kwantowych bitów), przez co nie jesteśmy w stanie przeprowadzać faktoryzacji dużych liczb. O tym, jak trudne to zadania może chociażby świadczyć fakt, że gdy w 1994 roku Peter Shor z Bell Laboratories przedstawił kwantowy algorytm rozkładu wielkich liczb na liczby pierwsze, to musiało minąć 7 lat intensywnych badań, zanim uczonym z IBM-a i Uniwersytetu Stanforda udało się przeprowadzić faktoryzację liczby 15. Zadanie to udało się dzięki miliardom miliardom cząsteczek, z których stworzono 7 kubitów. Jeśli chcielibyśmy złamać współczesny szyfr, musielibyśmy nauczyć się kontrolować tysiące kubitów.

Od 2001 roku poczyniono pewne postępy. Naukowcy używający adiabatycznego algorytmu kwantowego (AQC) dokonali faktoryzacji liczby 21. Teraz Chińczycy posunęli się znacznie dalej. Po raz pierwszy w historii dokonano kwantowej faktoryzacji trzycyfrowej liczby. Była nią 143.

Xu i jego koledzy również wykorzystali AQC. Metoda ta, w przeciwieństwie do algorytrmu Shora, nie polega na kolejnym wykonywaniu operacji obliczeniowych. Zamiast tego odnajduje ona hamiltonian (operator Hamiltona). Zawiera on wszystkie możliwe rozwiązania problemu, w tym to właściwe. Odpowiednio go przetwarzając można znaleźć stan podstawowy układu, w którym zawarta jest prawidłowa odpowiedź. W teorii wszystko dobrze działa, jednak jako że spektrum rozwiązań oferowanych przez hamiltonian rośnie wykładniczo wraz ze wzrostem długości liczby, praktyczne jej zastosowanie jest niezwykle skomplikowane i również wymaga kontrolowania dużej liczby kubitów.

Dlatego też Xu i jego zespół uprościli równania wykorzystywane przy pracy z hamiltonianem, zawężając w znaczącym stopniu spektrum możliwych odpowiedzi. Wykorzystaliśmy nową metodę i zredukowaliśmy liczbę kubitów potrzebnych do uruchomienia algorytmu, dzieki czemu mogliśmy przeprowadzić faktoryzację liczby 143 - mówi Xu.

Uczeni uważają, że ich podejście będzie przydatne również przy faktoryzacji większych liczb.

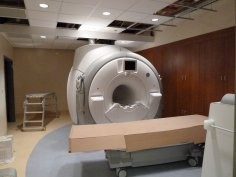
Chińczycy na potrzeby swoich badań użyli spektroskopu magnetycznego rezonansu jądrowego.