Rosną szanse na wykrycie „grudek” w jądrach atomowych

| Astronomia/fizyka
IFJ PAN

Jak naprawdę wyglądają jądra atomowe? Czy znajdujące się w nich protony i neutrony są rozmieszczone chaotycznie? A może łączą się w klastry alfa, czyli grudki zbudowane z dwóch protonów i dwóch neutronów? W przypadku kilku lekkich jąder doświadczalne potwierdzenie indywidualizmu bądź rodzinnej natury nukleonów będzie teraz łatwiejsze dzięki przewidywaniom przedstawionym przez fizyków z Krakowa i Kielc.

Każdy w miarę sumienny licealista dokładnie wie, jak wygląda jądro atomowe: to zlepek przypadkowo rozmieszczonych protonów i neutronów (czyli nukleonów). Sami fizycy nie mają jednak tak jednoznacznych wyobrażeń. Już w 1931 roku, zaledwie 20 lat po odkryciu jądra atomowego, pojawiły się pierwsze sugestie, że protony i neutrony w jądrach atomowych łączą się w jądra helu, a więc w grupki dwóch protonów i dwóch neutronów, często nazywane klastrami alfa. Jądra atomowe są jednak obiektami tak skrajnie małymi i trudnymi do zbadania, że choć od pierwszych przewidywań upłynął już niemal wiek, wciąż nie udało się jednoznacznie potwierdzić występowania w nich klastrów alfa.

Łączenie się obiektów w grupy sprzyja obniżaniu energii w układach fizycznych. Ten potężny, uniwersalny mechanizm występuje w przyrodzie w różnych skalach wielkości: kwarki łączą się w mezony lub bariony, atomy w cząsteczki, gwiazdy w galaktyki, a galaktyki w grupy galaktyk. W przypadku jąder atomowych symulacje komputerowe sugerują, że np. w jądrze berylu 9Be znajdują się dwa klastry alfa i jeden neutron (cały kompleks z wyglądu przypominałby hantel). W jądrze węgla 12C powinny znajdować się trzy klastry alfa (kształt jądra byłby więc trójkątny), cztery w tlenie 16O (tu jądro przypominałoby piramidę), dziesięć w wapniu 40Ca i czternaście w niklu 56Ni.

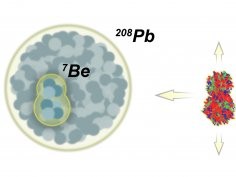
W 2014 roku naukowcy z Instytutu Fizyki Jądrowej Polskiej Akademii Nauk (IFJ PAN) w Krakowie, we współpracy z fizykami z Universidad de Grenada, przedstawili sposób wykrycia śladów pierwotnej struktury jąder atomowych w rozkładzie prędkości cząstek rozbiegających się z punktu zderzenia ultrarelatywistycznych lekkich jąder atomowych z tarczą zbudowaną z jąder ciężkich, takich jak ołów 208Pb czy złoto 197Au. Ówczesne przewidywania koncentrowały się wokół sposobów detekcji klastrów alfa w jądrach węgla 12C.

W naszej najnowszej publikacji, napisanej wraz z fizykami z Instytutu Fizyki Uniwersytetu Jana Kochanowskiego w Kielcach, przedstawiamy bardziej szczegółowe przewidywania dotyczące możliwości zaobserwowania śladów klastrów alfa w jądrach atomowych. Pokazujemy przy tym, jak klastry te można byłoby wykryć w kolejnych jądrach, nie tylko węgla 12C, ale także berylu 7Be i 9Be oraz tlenu 16O, mówi prof. dr hab. Wojciech Broniowski (IFJ PAN, UJK).

Metoda wykrycia klastrów alfa w jądrach atomowych, opisana w publikacji wyróżnionej przez redaktorów czasopisma Physical Review C, opiera się na ciekawej zależności. Ciężkie jądra atomowe, nawet gdyby składały się z klastrów alfa, są tak duże, że z dobrym przybliżeniem można je traktować jako dość jednorodne kule. Gdy w takie jądro z prędkością ultrarelatywistyczną (a więc bardzo bliską prędkości światła) uderza lekkie jądro atomowe, energia zderzenia jest tak wielka, że protony i neutrony na ułamki sekund rozpadają się na kwarki i zlepiające je gluony. Powstaje wówczas prawdopodobnie najbardziej egzotyczny płyn: plazma kwarkowo-gluonowa.

W naszej pracy zauważamy, że jeśli lekkie jądro atomowe nie jest jednorodne, obłok plazmy kwarkowo-gluonowej utworzony w wyniku zderzenia jest zdeformowany. Jego kształt przynajmniej w pewnym stopniu będzie odpowiadał kształtowi lekkiego jądra. Plazma będzie się więc rozlewała na wszystkie strony, ale w różnych kierunkach z nieco innymi prędkościami, wyjaśnia dr hab. Maciej Rybczyński, prof. UJK.

Plazma kwarkowo-gluonowa stygnie tak szybko, że bezpośrednie jej zaobserwowanie nie jest obecnie możliwe. Już po kilku femtosekundach (milionowych części jednej miliardowej sekundy) kwarki i gluony łączą się ponownie w cząstki w procesie nazywanym hadronizacją.

W kierunkach, w których plazma kwarkowo-gluonowa płynęła nieco szybciej, możemy się spodziewać nieco większych prędkości cząstek powstałych przy hadronizacji. Jeśli więc z dostateczną precyzją zarejestrujemy pędy cząstek rozbiegających się z punktu zderzenia, potencjalnie jesteśmy w stanie z drobnych różnic wydobyć informację o kształcie jądra, które uderzyło w tarczę. Na dodatek informacja ta będzie dotyczyła jądra w stanie podstawowym, tłumaczy Milena Piotrowska, doktorantka UJK.

Badania fizyków z IFJ PAN i UJK, współfinansowane z grantów Narodowego Centrum Nauki, dostarczają konkretnych przewidywań teoretycznych. Kolejny krok należy teraz do fizyków doświadczalnych pracujących przy akceleratorach o dużych energiach, takich jak Super Proton Synchrotron (SPS) czy Large Hadron Collider (LHC) w europejskiej organizacji CERN bądź Relativistic Heavy-Ion Collider (RHIC) w amerykańskim Brookhaven National Laboratory. Ponieważ eksperymenty potwierdzające grudkowatą strukturę jąder atomowych nie wymagają rozbudowy obecnie działającej aparatury, będzie można je przeprowadzić już w najbliższych latach.

Autor:

Źródło: Instytut Fizyki Jądrowej PAN

jądro atomowe klaster alfa nukleon jądro helu