Wystarczy 27 kuponów, by mieć gwarancję wygranej w Lotto - obliczenia matematyków z Manchesteru

| Ciekawostki
Dylan Nolte, Unsplash

Matematycy z Uniwersytetu w Manchesterze postanowili sprawdzić, ile kuponów trzeba wypełnić, by mieć gwarancję wygranej w brytyjskiej National Lottery. Doktorzy David Stewart i David Cushing stwierdzili, że wystarczy 27 kuponów, by z pewnością wygrać w Lotto, w której losowanych jest 6 z 59 liczb. Jednak, co ważne, nie jest to gwarancja najwyższej wygranej, a wygranej w ogóle, więc raczej nie odzyskamy pieniędzy wydanych na kupony.

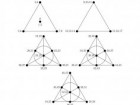
David Stewart, David Cushing, University of Manchester David Stewart, David Cushing, University of Manchester

Do swoich obliczeń naukowcy wykorzystali strukturę geometryczną o nazwie Płaszczyzna Fana. To zbiór punktów i prostych tworzących trójkąt. W Płaszczyźnie Fana każde dwie różne proste mają jeden punkt wspólny, a każde dwa różne punkty należą do jednej prostej. Wykorzystując tę koncepcję Stewart i Cushing wyliczyli, że potrzebują dwóch trójkątów i trzech Płaszczyzn Fana, by wykorzystać wszystkie 59 liczb i wygenerować 27 kuponów, w których będzie co najmniej jedna wygrana. Na załączonych grafikach liczby, którymi należy wypełnić kupon, leżą na tej samej prostej.

Jeśli w ten sposób wypełnimy kupony to, niezależnie od tego, które z ponad 45 milionów zestawów liczb zostanie wylosowanych, zawsze coś wygramy. W każdym bowiem z 45 milionów rozwiązań loterii musi znaleźć się co najmniej jedna z przedstawionych przez matematyków par, a to oznacza, że trafimy co najmniej najniższą z możliwych wygranych. Co ważne, istotna jest tu liczba 27 kuponów. Jeśli postanowimy zaoszczędzić i wypełnimy ich 26 to metoda nie zadziała.

Na 26 kuponach mamy miejsce na 156 skreśleń, a to oznacza, że wiele liczb wielokrotnie się nie pojawi. Co więcej, stwierdziliśmy, że w takim wypadku możemy znaleźć aż 6 liczb, które w ogóle nie znajdą się na żadnym z kuponów. Mówiąc językiem teorii grafów, dla 26 kuponów istnieje niezależny zbiór sześciu elementów, wyjaśnia doktor Stewart, wykładowca matematyki teoretycznej.

Naukowcy przypominają, że mimo iż ich metoda gwarantuje wygraną, to szanse na zysk są tak małe, że nie warto jej stosować. Wysłanie 27 kuponów będzie nas kosztowało 54 funty i w 99% przypadków nie odzyskamy tej kwoty.

Stewart i Cushing mówią, że praca, którą wykonali, to interesujący problem obliczeniowy. Wykorzystali przy tym liczący sobie ponad 50 lat język programowania Prolog, jeden z najpopularniejszych języków programowania logicznego.

Autor:

Źródło: University of Manchester

Lotto wygrana kupony